PID
Control Theory
What is PID?
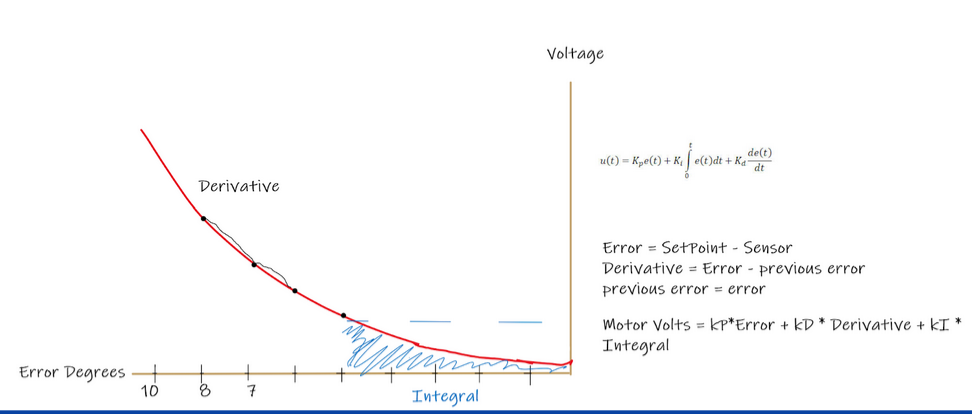
PID is an acronym for Proportional Integral Derivative. A key algorithm in control theory. A PID allows you to slow an approach to reach a target and minimize overshoot and undershooting. This algorithm has wide uses from robotics to thermostats.
You can think of a PID as representing the error between the start position and the target. By breaking this total into smaller parts following calculus principles you can gain the derivative and integral. This algorithm is highly customizable allowing fine tuning for unique problems and solutions.
PID’s are mainly used in a closed loop system where you want it to end at the target. The three gains need to be tuned for each system.
For instance in my use I used PID throughout my robotics experience to increase the accuracy of approaching a target position or angle. With my implementation the robot error approaches 0 then begins to use the integral values to push it that last leg of the approach.
This algorithm can be done with several sensors depending on use. For my use I used the Vex v5 inertial sensor. It was used to reliably turn to face an absolute angle in refernence to the starting angle being 0 (though this can easily be adjusted). My implementation allowed the robot to slow down as it approached a target and turn back if the angle is overshot and parameters are tuned correctly.
As far as the range of kI,kD,kP for Vex go, typically kP is between .1 and .2, kD is between .01 and kP, kI is usually close to kD minus a magnitude.
Original PID Code
// Used to count the number of turns for output data only
int turnCount = 0;
// Relative degree tracking
int angleTracker = 0;
// Weighted factor of porportion error
double kP = 0.19;
// Weighted factor of integral error
double kI = 0.01;
// Weighted factor of the derivated error
double kD = .1;
// Max speed in Volts for motors
double maxSpeed = 6;
// The angle difference from error when integral adjustments turns on
int turnThreshold = 16;
// Tolerance for approximating the target angle
double turnTolerance = .5;
// Total number of iterations to exit while loop
int maxIter = 300;
// Turning Function
void turnPID(double angleTurn) {
// Distance to target in degrees
double error = 0;
// Error degree from the last iteration
double prevError = 0;
// Derivative of the error. The slope between iterations
double derivative = 0;
// Accumulated error after threashold. Summing error
double integral = 0;
// Iterations of the loop. Counter used to exit loop if not converging
double iter = 0;
// Automated error correction loop
while (fabs(TurnGyroSmart.rotation(degrees) - angleTurn) > turnTolerance && iter < maxIter) {
iter += 1;
error = angleTurn - TurnGyroSmart.rotation(degrees);
derivative = error - prevError;
prevError = error;
// Checking if error passes threshold to build the integral
if (fabs(error) < turnThreshold && error != 0) {
integral += error;
} else {
integral = 0;
}
// Voltage to use. PID calculation
double powerDrive = error * kP + derivative * kD + integral * kI;
// Capping voltage to max speed
if (powerDrive > maxSpeed) {
powerDrive = maxSpeed;
} else if (powerDrive < -maxSpeed) {
powerDrive = -maxSpeed;
}
// Send to motors
LeftDriveSmart.spin(forward, powerDrive, voltageUnits::volt);
RightDriveSmart.spin(forward, -powerDrive, voltageUnits::volt);
this_thread::sleep_for(15);
}
// Angle achieved, brake robot
LeftDriveSmart.stop(brake);
RightDriveSmart.stop(brake);
// Tuning data, output to screen
turnCount += 1;
error = angleTurn - TurnGyroSmart.rotation(degrees);
derivative = error - prevError;
Controller1.Screen.clearScreen();
Controller1.Screen.setCursor(1, 1);
Controller1.Screen.print("Turn #: %d", turnCount);
Controller1.Screen.setCursor(1, 13);
Controller1.Screen.print("iter: %.0f", iter);
Controller1.Screen.newLine();
Controller1.Screen.print("error: %.5f", error);
Controller1.Screen.newLine();
Controller1.Screen.print("derivative: %.5f", derivative);
Controller1.Screen.newLine();
}
The above code was the original turning PID structure for a blocking function in the Vex V5 system.
Furthur Development
During my competition seasons with Vex I observed the need for a second PID. If my first PID came about to solve the inacuracy observed in a robot’s turning then the second came about similarly. When the robot drove forward to meet a certain target distance the wheels would often slip leading to inaccuracy. Thus I reimplementated a PID to drive for a target distance.
This PID originally worked for Vex V5 IME’s in the V5 motors. This was eventualy improved to use the Vex Quad Encoders on a dead wheel. The dead wheel was designed to be a free spinning wheel with a sensor attached connected to the chassis along a pivot with a tension mechanism in the form of a rubber band. This would minimize tracking slippage in data increasing accuracy. To increase accuracy the driving PID used degrees for internal units. This meant a user could call the function for 12 inches and the program would do the math in rotational degrees of the wheel. The accuracy for a well tuned drive PID model would be within .3 of an inch of a target.
By implementing several PID’s in the Vex system I created an understanding of the basics of control theory. Having learned the key underlying structure of the base algorithm it can be implemented in various other settings.
I eventually created a third PID that functioned with Odometry to both turn and drive to a target coordinate point at the same time. During this time I refactored my previous algorithms to use object orientation and create a more simplistic structure.
Final Code Iteration
#define wheelDiameter 3.25
//Setters and getters
void PID::setMaxSpeed(double s){
maxSpeed=s;
}
void PID::setMaxIter(int i){
maxIter=i;
}
void PID::setTurnThresh(int t){
turnThreshold=t;
}
void PID::setTurnTolerance(double tol){
turnToTolerance=tol;
}
void PID::setkI(double I){
kI=I;
}
void PID::setkD(double D){
kD=D;
}
void PID::setkP(double P){
kP=P;
}
void PID::setiBound(double b){
iBound=b;
}
void PID::setThreshold(double t){
threshold=t;
}
double PID::getXVector(){
return xVector;
}
double PID::getYVector(){
return yVector;
}
double PID::getBRPower(){
return BackRightPower;
}
double PID::getBLPower(){
return BackLeftPower;
}
double PID::getFRPower(){
return FrontRightPower;
}
double PID::getFLPower(){
return FrontLeftPower;
}
void PID::setMaxSpeedT(double s){maxSpeedT=s;}
void PID::setkIT(double I){kIT=I;}
void PID::setKDT(double D){kDT=D;}
void PID::setkPT(double P){kPT=P;}
void PID::setiBoundT(double b){iBoundT=b;}
void PID::driveToNS(Odometry &Odom) {
//ns and turn to need different pid values in same instance and need to call odom functions from odom object
error = sqrt(pow(yTargetLocation - Odom.getYPosGlobal(),2)+pow(xTargetLocation-Odom.getXPosGlobal(),2));
derivative = error - prevError;
prevError = error;
if(fabs(error) < iBound && error != 0) {
integral += error;
} else {
integral = 0;
}
powerDrive =((error * kP) + (derivative * kD) + (integral *kI));
if (powerDrive>maxSpeed) {
powerDrive=maxSpeed;
}
}
//This turn to PID is specifically for the Odometry movement because it relies on vectors instead of a target angle
void PID::turnTo(Odometry &Odom) {
errorT = ((atan2(yVector,xVector))-Odom.getAbsoluteAngle());
derivativeT = errorT - prevErrorT;
prevErrorT = errorT;
// turnPID.iBound = .2;
//turnPID.threshold = 0.5; cause its in radians here
if (fabs(errorT) < iBoundT && errorT != 0) {
integralT += errorT;
} else {
integralT = 0;
}
powerDriveT = (errorT * kPT) + (integralT * kIT) + (derivativeT * kDT);
powerDriveConT=ConvertToDeg(powerDriveT);
if (powerDriveConT > maxSpeedT) {
powerDriveConT = maxSpeedT;
} else if (powerDriveConT < -maxSpeedT) {
powerDriveConT = -maxSpeedT;
}
}
void PID::turnPTo(double angleTurn) {
iter=0;
// Automated error correction loop
//Loop runs every 15 miliseconds
//This function is in degrees internally and externally
//while the error is less than thresholds and the amount of times in the loop is less than threshold
// This is to account for when you haven't reached your target but the robot is stuck it may exit the loop
while (fabs(TurnGyroSmart.rotation(degrees) - angleTurn) > turnToTolerance && iter < maxIter) {
iter += 1;
//The error is the target angle - current angle
error = angleTurn - TurnGyroSmart.rotation(degrees);
//The derivative is the error-previous error
//These are defined as 0 before the loop runs
derivative = error - prevError;
//Then change the previous error value to the error before the next loop
prevError = error;
// Checking if error passes threshold to build the integral
//The integral allows you to correct for overshooting so you don't want this to always run
if (fabs(error) < turnThreshold && error != 0) {
integral += error;
} else {
integral = 0;
}
// Voltage to use. PID calculation
double powerDrive = error * kP + derivative * kD + integral * kI;
// Capping voltage to max speed
if (powerDrive > maxSpeed) {
powerDrive = maxSpeed;
} else if (powerDrive < -maxSpeed) {
powerDrive = -maxSpeed;
}
// Send voltage to motors
LeftDriveSmart.spin(forward, powerDrive, voltageUnits::volt);
RightDriveSmart.spin(forward, -powerDrive, voltageUnits::volt);
this_thread::sleep_for(10);
}
// Angle achieved, brake robot
LeftDriveSmart.stop(brake);
RightDriveSmart.stop(brake);
// Tuning data, output to screen
turnCount += 1;
error = angleTurn - TurnGyroSmart.rotation(degrees);
derivative = error - prevError;
Controller1.Screen.clearScreen();
Controller1.Screen.setCursor(1, 1);
Controller1.Screen.print("Turn #: %d", turnCount);
Controller1.Screen.setCursor(1, 13);
Controller1.Screen.print("iter: %.0f", iter);
Controller1.Screen.newLine();
Controller1.Screen.print("error: %.5f", error);
Controller1.Screen.newLine();
Controller1.Screen.print("derivative: %.5f", derivative);
Controller1.Screen.newLine();
}
void PID::driveToP(Odometry &Odom,double xTarget, double yTarget, double alpha,double beta) {
//the x and y target converted to degrees traveled
xTargetLocation = (xTarget*360)/(M_PI*wheelDiameter);
yTargetLocation = (yTarget*360)/(M_PI*wheelDiameter);
//the difference between targets - current
xVector = xTargetLocation - Odom.getXPosGlobal();
yVector = yTargetLocation - Odom.getYPosGlobal();
//while loop of the vector needed to travel and the angle left to turn
//once below threshold should exit
while(sqrt(xVector*xVector+yVector*yVector)>26 || (atan2(yVector,xVector)-Odom.getAbsoluteAngle()) >=ConvertToRadians(5) ) {
xVector = xTargetLocation - Odom.getXPosGlobal();
yVector = yTargetLocation - Odom.getYPosGlobal();
//Activate 2 subPIDs
PID::driveToNS(Odom);
PID::turnTo(Odom);
//the drive power for each motor
//combines the drive and turn using alpha to determine the ratio
//1=alpha is all turn 0=alpha is all drive
FrontLeftPower = beta*(alpha*powerDrive -(1-alpha)*powerDriveCon);
BackLeftPower = beta*(alpha*powerDrive-(1-alpha)*powerDriveCon);
FrontRightPower = beta*(alpha*powerDrive + (1-alpha)*powerDriveCon);
BackRightPower = beta*(alpha*powerDrive +(1-alpha)*powerDriveCon);
//sends velocity in volts to each motor to actually drive
FrontLeft.spin(forward,FrontLeftPower,voltageUnits::volt);
FrontRight.spin(forward,FrontRightPower,voltageUnits::volt);
BackLeft.spin(forward,BackLeftPower,voltageUnits::volt);
BackRight.spin(forward,BackRightPower,voltageUnits::volt);
//print data to console for checking
printf( " \n");
printf( "xPos %.5f\n", Odom.getXPosGlobal());
printf( "yPos %.5f\n", Odom.getYPosGlobal());
printf( "sqrt %.5f\n", sqrt(xVector*xVector+yVector*yVector));
printf( "atan2 %.5f\n", atan2(yVector,xVector)-Odom.getAbsoluteAngle());
printf( "targethe %.5f\n", atan2(yVector,xVector));
printf( "ytarget %.5f\n", yTargetLocation);
printf( "xtarget %.5f\n", xTargetLocation);
printf( "FLP %.5f\n", FrontLeftPower);
printf( "currtheta %.5f\n",Odom.getAbsoluteAngle());
printf( "turn pd %.5f\n", powerDriveCon);
printf( "drivepid pd %.5f\n", powerDrive);
printf( "New Iteration00 \n");
printf( " \n");
if (fabs(xVector) <=15 && fabs(yVector) <= 15 ){//&& atan2(yVector,-xVector)-absoluteAngle-M_PI/2<=ConvertToRadians(4)){
printf("exit \n");
break;
}
task::sleep(15);
}
//once while loop is not true stop motors
FrontLeft.stop();
FrontRight.stop();
BackRight.stop();
BackLeft.stop();
}
The code above depicts this refactor and expansion in Vex CPP. Here is an example of the turn PID running.